Using Ten's Complement to Represent Negative Numbers
A look at how mechanical computation devices deal with negative numbers

Binary digital computers represent negative numbers using something called two's complement. The reason is simple: Memory cells can store zeros and ones, but not a negative sign. But instead of explaining two's complement, I am going to explain ten's complement. Why? Because it helps you understand how computers work with negative numbers without having to learn the binary number system. It is also a natural followup to my stories about decimal based computation using the Abacus and the Arithmometer (mechanical calculator). In neither story did I explain how one represents negative numbers. Time to amend that.
An Arithmometer perform addition and subtraction using rotating gears, which means any operation which produce a negative number behaves similar to analog clocks. If the hour hand shows two and you subtract three hours, you end up with eleven. A mechanical counter as the one shown below works much the same way.
The green mechanical counter has four digits. If it shows 3, and you click the counter four times, you end up with 7. In other words, you can perform addition. What happens when the counter says, 9998, and you click 4 times? You get a wrap around and end up with 2. In other words, 9998 acted as -2. There is a clear pattern. 9999 acts as -1, 9998 as -2, 9997 as -3 and so on. We are using the ten's complements to represent negative values. If you want to represent -4, you pick the complement of 4 which is 6.
This idea can be expanded to more digits. If you have n digits and want to find the ten's complement k of number x you perform the following calculation:
k = 10ⁿ - xLet us say n = 2 , meaning we would like to find the ten's complement of a two-digit number. Let us say we want to represent -6. Our calculation gives:
k = 10² - 6 = 100 - 6 = 94A mechanical counter or calculating machine will naturally wrap around to treat these numbers as negative numbers by virtue of their mechanical design. However, if we would like to simulate the calculation ourselves, then we need to perform what is called modular arithmetic.
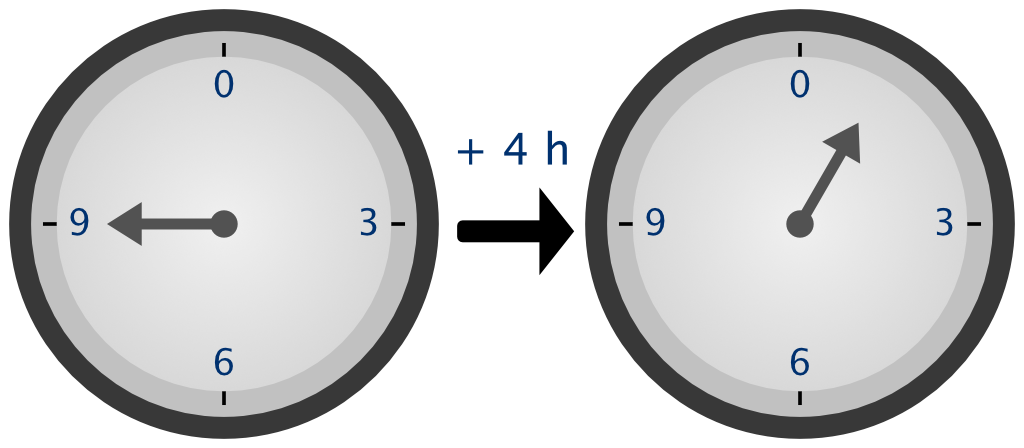
Modular arithmetic treats numbers the same way we treat numbers when doing time calculations. Here is an example of modular arithmetic.
03 mod 12 = 3
04 mod 12 = 4
16 mod 12 = 4
17 mod 12 = 5Instead of using 12 as base, we can use 10. You can see that 96 is acting like -4 because when we add it to 14 we get 10 as a result when using modular arithmetic.
96 + 14 mod 10² = 10
04 + 12 mod 10² = 18Modular arithmetic is closely related to calculating the remainder from an integer division. 96 + 14 is 110. If we divide 110 by 100 we get 10 as the remainder. It is the same deal when working with an analog clock. If you divide 15 by 12, then the remainder is 3.
For positive values the modulus and remainder are the same. Hence all these examples will tend to work with the
%operator in programming languages such as Python, Julia, JavaScript, Java, C/C++, Go and C#. In Julia you can call theremormodfunctions to distinguish the closely related operations.
How do you determine if a number is negative?
You can use the number 52 to represent the negative number -48 for 2-digit calculations, but when a calculation produce 52 as a result, then how do you know if that represents -48 or 52? In principle, you cannot tell. In practice, we divide the possible value range of a double-digit number into a positive and negative range. That means if we work with 2-digit numbers, we might decide that numbers from 50 to 99 represents the range -50 to -1, while numbers from 0 to 49 represent positive values. If we work with 3-digit numbers, we would instead make 500 to 999 represents -500 to -1. Hopefully, you can see the pattern.
If you know binary numbers, then this example gives you a hint as to why an 8-bit number can either represent unsigned values from 0 to 255 or signed values from -128 to 127. How you define this range is up to the implementer of the computer hardware. For instance, in my imaginary mechanical computer, the Calcutron-33, different arithmetic operations define different ranges. When using a single digit, I map numbers from 0 to 9 to the range -5 to 4. However, for some operations, I map single digit numbers to -2 to 7. What are the practical implications?
It matters when you want to expand a single digit number to a larger digit number and need to do what is called sign-extension. For instance, if working with single digit numbers, then an 8 would typically mean -2. We cannot expand this number to four digits by just slapping on zeros because that gives us 0008, which would count as positive 8. To make it still work as a negative number, we need to add nines and get 9998. The choice of whether nines or zeros should be added is determined by what range you have defined. If the range is -5 to 4, then you add nines if the number is larger or equal to five. However, if the range is -2 to 7, that choice only happens when the number is larger or equal to eight.
Why is any of this useful to know?
My path to explore ten's complement and representation of negative numbers in computer hardware began with creating an imaginary decimal-based computer, the Calcutron-33. My motivation was to create computer hardware that was easy to understand for beginners. It is a bit like learning to drive with an automatic transmission instead of stick shift. You can focus on learning how to drive safely, observe signs and change lanes instead of having too much of your attention focused on the mechanics of how a stick-shift works. This is the same basic idea. Learn all the key low-level elements of a computer without having to also deal with the binary number system at the same time.
Knowing how ten's complement works makes it much easier to understand two's complement and sign-extension with binary numbers. Anyone who wants to get their hands dirty with assembly programming will need to learn both concepts at some point.
Assembly programming may seem horrible outdated today. Indeed, I am not suggesting you write the next web browser in assembly code. However, knowing the basics of assembly code and how compilers create it helps give you a more profound understanding of the high-level programming languages we use daily. Donald Knuth, who is among the most renowned computer scientists alive today, thinks this is essential. It is for this reason that his epic book series: The Art of Computer Programming covers algorithms and their implementation using assembly language. His point is that only if you express algorithms in assembly code can you truly get a sense of the performance implications of different algorithm implementations.

However, the assembly code Donald Knut uses isn't based on an actual existing microprocessor but an imaginary processor which is well suited for teaching (the MMIX processor). The idea was to describe algorithms in a timeless manner, so that regardless of what hardware looks like in 20 years, his books will still be relevant. I always found the challenge of making something that can stand the test of time interesting.
I once listened to the designers of the Bugatti Chiron. It is a supercar for collectors. Like Swiss watches, they are meant to have an enduring quality. The designers knew that if they put in something like a fancy electronic display, it would quickly get outdated. The controls on the Bugatti Chiron is thus far more physical. It is much the same reason why expensive Swiss watches that people collect are all mechanical rather than digital. Digital watches do not have an enduring quality. You cannot make a timeless digital watch because the technology will look totally outdated in few years.
Calcutron-33 is likewise meant to be something that is useful 10 or 20 years from now, assuming processors are still built upon RISC principles.





