From Abacus to Microprocessors
Understanding modern technology by learning about old technology
If you study the operations of a modern microprocessor, you might notice similarities between it and old mechanical calculating devices such as the Arithmometer if you squint hard. To be more specific, what we call the Arithmetic Logic Unit (ALU) in a microprocessor has many similarities with old mechanical calculators. The ALU can be thought of as the calculator of a microprocessor. It reads numbers stored in registers, perform addition, subtraction, or a shift operation and store the result back into another register. A register is a thing that can hold a number.

These basic operations are exactly the same ones performed by an Arithmometer. It has three registers to hold numbers used during calculations:
Input Register – A 5-digit register where you pull small levers to define an input number.
Accumulator Register – A 13-digit register for holding the result of multiple calculations.
Counter Register – An 8-digit register to keep track of how many additions or subtractions you have performed.
I will not explain either a microprocessor ALU or an old mechanical calculator in much detail here. Instead, we will travel even further back in time to the Abacus. Different forms of these manual calculating machines have existed since before Roman times.
Why learn about the Abacus and its operation? Is it not completely outdated and useless? Because understanding the Abacus helps you see the big picture. There is something very satisfying about being able to connect the dots between ways of working with numbers thousands of years back and our modern approach using microprocessors. Modern microprocessors are so complex that you easily get lost in the non-essentials, when trying to understand them.
An Abacus, just like the ALU of a microprocessor, has limitations on the number of digits they can work with. Modern computers are based on the binary number system, where each digit is called a bit. The first computer I encountered growing up in the 1980s was a Commodore 64. It had an 8-bit microprocessor called the 6502. It means it could work with numbers of up to eight binary digits. The Abacus I have illustrated below can work with numbers of up to four decimal digits. Every column on the Abacus represents a digit in a number.
The first column starting from the right is the ones. The second column is the tens, the third column the hundreds and so on. That means if I want to represent the number 4023 on an Abacus, then I arrange the beads as shown in the illustration above. With this arrangement, addition and subtraction is easy to perform. If I would like to add 12, I just pull down two extra beads in the ones column and one bead in the tens column.
Adding and subtracting is quite trivial, so let us look at how multiplication is done on an Abacus. Multiplication is done in a very similar fashion to how multiplication is done with old mechanical calculators and early microprocessors, which only had ALUs and not dedicated multiplier hardware. In fact, small microcontrollers such as the 8-bit AVR chips used on popular Arduino boardstoday still perform multiplication using an algorithm similar to the one I will show here.
Multiplication with an Abacus
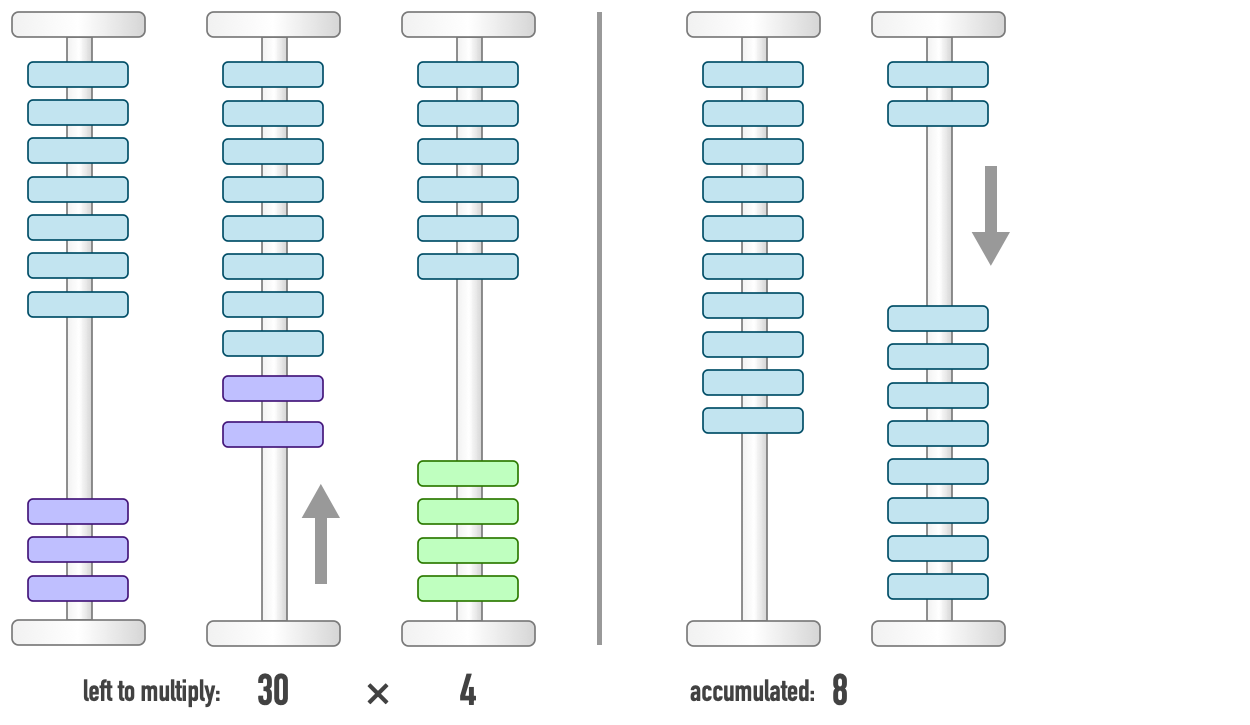
In this example, we will do a simple multiplication: 32 × 4 which should yield 128. To carry out this operation, we assign specific meaning to each column. The first two columns are turned into the counter register, while the third column is defined as an input register. Finally, we let the two last columns be the accumulatorregister, which will hold the final result.
Multiplication can be thought of as performing numerous additions. In our example, we will be adding four 32 times to perform multiplication. Naturally, it would be much faster to perform the reverse: Adding 32 four times. The reason we will not do that in this example is because doing it the opposite way is more educational. It helps explains the mechanism used better.
Multiplying with the Ones Column
We start by adding four once to the accumulator. Four beads in the ones-column are moved down. To keep track of how many additions of four we have done, we remove one bead from the counter. In effect, we start at 32 and count down towards zero.
We add four once more to the accumulator, reducing the counter to 30. At this point, the accumulator holds the value eight. We have 30 more additions of four to go.
Multiplying with the Tens Column
Moving four beads on the ones column 30 more times would be tedious. Fortunately, we don't have to. Instead, we perform a shift operation to speed up our additions. We let every moved bead count as ten times four. How does that work? Every time we move a bead in the tens column of the counter, we move four beads in the tens column of the accumulator. Performing this operation once reduce the counter from 30 to 20 and the accumulator is increased to 48 (8 + 4 × 10).
We repeat the same operation once more, thus reducing the counter from 20 to 10 and adding another 40 to the accumulator, which now holds the value 88 (48 + 4 × 10).
Notice in the diagram above that we cannot move down another four beads because only two beads remain in the tens' column of the accumulator. We need to use a third column with the accumulator representing hundreds. We trade ten of the beads in the tens' column for one bead in the hundreds' column.
Furthermore, we need 12 beads in total from the tens' column, which we trade in for 1 bead in the hundreds column and 2 beads in the tens' column. At this point, we have spent all the beads in the counter, and we are done. We can see that the final result is 128.
Shift Operations
Multiplying and dividing directly cannot be done either with an Abacus, mechanical calculator or ALU. We can, however, easily multiply with multiples of 10. Multiplying an input number with 10, 100 or 1000 is easy: all you have to do is move beads 1, 2 or 3 columns over. Doing 2 × 4 requires you to move four beads in the ones column twice. If instead you want to perform 20 × 4, you move four beads twice in the tens column. If it is 200 × 4, it means moving eight beads in the hundreds column. What you are doing in essence is a combination of addition and shift operations.
If you look at an Arithmometer, you will see that the accumulator register is located on a sliding bar. Slide the bar one notch to the left, and the number added from the input register will be ten times larger. Slide the bar two notches to the left and the input will become one hundred times bigger. We can slide the bar to the right to make the added numbers smaller. An interesting effect of sliding the bar doing the carriage shift is that it also affects the counter register. Say you specify the input register to be 42. Next, slide the bar two notches to the left. When you crank the handle to add the input to the accumulator you would be adding 4200. The counter will show 100. Thus, it looks the same as if you had cranked the handle one hundred times. In other words, shifting allows us to dramatically reduce the number of times we perform additions.
However, these shift operations are no different from what we can achieve on an Abacus. The key difference is that you need to update the accumulator and counter yourself by manually moving beads around.
Use of Shift Operations in Microprocessors
Shift operations help us speed up multiplication and division on the ALU of a microprocessor. Because a modern microprocessor operates with the binary number system, shift operations multiple inputs with multiples of two. Thus rather than multiplying inputs with 10, 100, 1000 or 10 000, we multiply with 2, 4, 8, 16, 32 and so on.
This kind of knowledge was actually useful when I started programming. I got into programming because I wanted to make games. In the early 1990s, PCs did multiplication very slowly. In principle, we had to use multiplication to calculate the position of a pixel in graphics memory at a specific x, y coordinate. Since the screen resolution was 320 × 240, you had to multiply the y-coordinate with 320 and add the x-coordinate to get a location in screen memory.
If this sounds like gobbledygook to you, don't worry. The key takeaway is that I had to multiply an arbitrary number y with 320 numerous times. This was very slow because multiplier hardware in PCs back then sucked. The solution was changing the calculation to a combination of shifts and additions. Here is a walk through:
f(x, y) = 320y + x = (16 * 20)y + x
f(x, y) = (2⁴ * 2*2*5)y + x = (2⁶ * 5)y + x
f(x, y) = (2⁶ * (2² + 1))y + x
f(x, y) = (2⁸ + 2⁶)y + x
f(x, y) = 2⁸y + 2⁶y + xIn other words, you can left-shift your input y eight times and add the result of left shifting the same input six times. In other words, you replace a multiplication with two shift operations and an addition. Back then, that gave a crucial speed improvement when doing computer graphics.
Next time, we will study mechanical calculators more in detail. My intention with these stories is to provide background material for anyone interested in learning assembly programming and who are curious about the bigger picture.