The Calcutron-33 Instruction-Set

Coverage of all the Calcutron-33 assembly instructions version 3.x

If you want to program the Calcutron-33 CPU, my made up decimal number based RISC-like microprocessor, you need to know what instructions it supports and how they work. To get you started, let us look at a simple example of a Calcutron-33 program. It contains several instructions such as INP, BGT and JMP. In addition, there are labels such as loop, second and first. The latter are not instructions, but ways to refer to different locations in the program.

loop:
    INP  x1
    INP  x2
    BGT  x1, x2, first

second:
    OUT  x2
    JMP loop

first:
    OUT  x1
    JMP loop
    HLT

This program keeps reading pairs of numbers from its input using the INPinstructions. The read numbers are stored in the x1 and x2 registers, respectively. Next, we compare the numbers in the x1 and x2 registers using the BGTinstruction. BGT is shorthand for: "Branch if Greater Than." If the first operand x1 is greater than the second operand x2, the program jumps to the first label. Here there is an instruction OUT x1 which writes the contents of the x1 register to output.

BGT is what we call a conditional branch instruction. Conditional branch instructions evaluate a condition and if the condition is true, the microprocessor will jump to a new location in the program. Not all jumps are based on a condition being true. For instance, the JMP loop instruction will jump to the loop label without evaluating any condition. The jump always happens.

If you study the program, you can see that the purpose of the BGT instruction is to decide whether we should run the OUT x2 or OUT x1 instruction. The program has been made so that whatever register x1 or x2 which holds the higher value will be written to the output.

To be able to understand this program and others, it is useful to have a full overview of the instructions that exist for Calcutron-33. All operands follow a similar format to what you can see below:

First you have a mnemonic which will get translated to single digit opcode. Next follows the operands. Each operand is encoded as a single or double-digit number.

Instruction-Set Overview

The diagram below show all supported Calcutron-33 instructions, how they are encoded as machine code and what they do. The rightmost part under an orange header is special. It is a list of so-called pseudo instructions. These instructions are really just shorthand for variants of the actual 10 instructions, which are possible with a single decimal digit for opcode. Rd, Ra and Rb refers to operands which can be either one of the registers x0 to x9. The k represent an immediate value (a constant encoded directly in the instruction). You can look at the encoding to see if the k represent a single digit or two-digit immediate value.

The encoding notation should be easy to read. The ADDI Rd, k instruction for instance is encoded as 2dkk. The number 2 is the opcode for the Add Immediate value instruction. d means we use a single decimal digit to encode the destination register Rd for the operation. kk tells us that two digits are used to encode the constant value k. That means you can use values up to 99 with ADDI. The left shift operation LSH in contrast is encoded as 4dak which inform you that the largest immediate value k which you can encode is 9. In fact, it is lower than that because we need to be able to represent negative values as well. 9 to 5 is typically used to represent -1 to -5, while 0 to 4 represents positive values.

If you don't know how we represent negative numbers in memory, I suggest you read my earlier coverage of the topic: Using Ten's Complement to Represent Negative Numbers

The descriptions use arrow symbols, such as ← to show where the result of an operation is stored. The equal symbol = is to show comparison. For instance, in the description of the BEQ Ra, Rb, k instruction you see the following description:

if Ra = Rb
   PC ← PC + k

That means that if register Ra equals register Rb we add the constant value kto the program counter (PC) and store the result in the program counter. Since the program counter is used to keep track of where we are in our program, this has the effect of performing a jump to another location in the program.

Let us look at an example to clarify:

    BEQ x3, x4, output
    HLT

output:
   OUT x4
   HLT

If the number contained in register x2 and x4 are equal, we jump to instruction OUT x4. When this program is assemble, the BEQ instruction will get encoded as 0342. The first digit zero is the opcode for BEQ. Next follows the digits 3 and 4 representing the registers x3 and x4. The branch instruction use relative addresses. So, the third operand is encoded as 2 because we need to jump two instructions forward to get to the output label.

Register File

Since a single decimal digit is used to encode source and destination registers, we have in theory 10 addressable registers. However, only the registers x1 to x9 can be used to store numbers. Register x0 is a kind of dummy register which always holds the value 0. This is a popular choice on many RISC instruction-sets. You will find this on MIPS and RISC-V. On 64-bit Arm microprocessors, the zero register is register x31.

Having one register always be zero is very practical. For instance, if I want to load a number from memory address 5, into register x4, I can write LOAD x4, x0, 5. If I didn't have a zero register, I would have to clear a register holding the second operand Rb first. When looking at pseudo instructions, you will see more good examples.

Most of the arithmetic and logical operations are self-explanatory. They all involve using the ALU to perform operations. The shift instruction requires a bit of explanation. When k > 0 you perform a left-shift, meaning the Ra register is made larger. When k <0 a right-shift is performed on Ra which corresponds to division by multiples of ten.

Conceptual explanation of a left and right shift operations on the decimal number 423

You cannot shift more than four places, so k has to be in the range -4 to 4. Digits that "spill over" from a shift are stored in the Rd register. Allow me to clarify with an example. Let us say register x1 contains the number 4321, and you execute the following instruction:

LSH x2, x1, 2

Shifting 4321 two places to the left results in the number 2100 in register x1 because all Calcutron-33 registers are 4-digits wide. Meanwhile, register x2 will contain the number 0043. Assuming we instead had performed the following operation:

LSH x2, x1, -1
RSH x2, x1,  1   // identical operation

Guess what register x2 and x1 will contain now. x1 will be reduced to 0432 and x2 will contain 0001.

When reading the description of the load and store operations, you have to think of M as being an array representing main memory. So M[addr] means getting the value at address addr. With Calcutron-33, the memory addresses are formed by combining the value of a register Ra and a single digit constant k.

Say you want to load the contents of address 20, 21 and 22 respectively into register x2, x3 and x4. How would you do it? The addresses are too big to hold in k alone. A naive approach would be to write:

LODI x1, 20        // LOaD Immediate
LOAD x2, x1, 0
LODI x1, 21
LOAD x3, x1, 0
LODI x1, 22
LOAD x4, x1, 0

But you can save instructions by using k as an offset, like this:

LODI x1, 20
LOAD x2, x1, 0
LOAD x3, x1, 1
LOAD x4, x1, 2

You may ask: Why make it so complicated? Why not just let the user write LOAD x1, 20 and LOAD x2, 21? What if you want to add 40 numbers located at memory address 20 to 60? You could write something like:

// not valid Calcutron-33 code
LOAD x1, 20
ADD  x2, x2, x1
LOAD x1, 21
ADD  x2, x2, x1
LOAD x1, 22
ADD  x2, x2, x1

// ... you get the idea

Obviously, this approach would require far too many instructions. Instead, what you want is to shorten the program using a loop:

   LODI x3, 20    // start address
   LODI x4, 60    // end address
next:
   LOAD x1, x3, 0
   ADD  x2, x2, x1
   ADDI x3, 1
   BLT  x3, x4, next
   OUT  x2        // write out result
   HLT

Now we only need 6 instructions to add 40 numbers. That is why using a combination of register value and constant value to calculate an address to read or write is so useful.

The JMP instruction is unconditional, meaning it happens regardless of what value registers contain. All instructions starting with a B such as BEQ and branch instructions, and they are conditional jumps. A conditional jump means that some comparison between two registers is done to decide whether a jump to a given address should happen.

Both the conditional and unconditional jumps have significant restrictions you need to be aware of. The JMP instruction makes jumps to absolute addresses. For instance, JMP x0, 32 would jump to the instruction at address 32. In contrast, BEQ x0, x0, 4 doesn't jump to address 04 but to address PC + 4. In other words, it jumps four instructions forward from the current location. That means you can also write negative values for jumps. Instruction BEQ x0, x0, -1 jumps one instruction back.

You can only jump five instruction backwards or four instructions forward. That is quite limiting, which means you will occasionally need to use JMP instructions. The example code examples/fastmult.ct33 in the Calcutron-33 GitHub repoperform multiplication through a combination of shifts and addition. A challenge I had when writing this code was that I had to carry out more instructions than I could fit in a loop. Don't worry if this code doesn't make sense. What I want you to note is that there is a JMP x9, multiply because the BGT x2, x0, nextwouldn't work if we squeezed in the instructions under multiply in where the JMP instruction is located. The next label cannot point to an instruction more than 5 instructions back.

loop:
    INP x1
    INP x2
    CLR x4
next:
    RSH x3, x2, 1     // divide by 10, remainder in x3
    CLR x9            // add x9 to form jump address
    JMP x9, multiply
    LSH x0, x1, 1     // make multiplicand 10x bigger
    BGT x2, x0, next  // process next digit
    OUT x4
    JMP loop          // next pair of numbers to multiply
    HLT


multiply:
    BEQ  x3, x0, skip
    ADD  x4, x1
    DEC  x3            
    BGT  x3, x0, multiply
skip:
    JMP x9             // return from subroutine

The JMP instruction itself is wonky because I squeezed in two instructions into one. We need the ability to return from a subroutine call.

Subroutine – A collection of instructions to carry out a task. It can be jumped to from several locations in the main program. Designed so that one can return after task has been carried out.

For instance, in theory, multiply could be jumped to from multiple locations. How do you get back to the instruction following the call? We do that by storing the return address in a register. JMP x9, multiply stores the address of the successive shift instruction LSH x0, x1, 1 into register x9. In theory, we could have expanded the instruction-set with another jump instruction using a register to hold the destination address. Except we only have a single decimal digitfor opcodes, and I spent them all. The solution is to make JMP a chameleon: The jump address is specified as x9 + multiply. That is why it is necessary to clear the x9 register before making the jump, or the address will be all wrong. The return from the subroutine is written JMP x9 which is just short for JMP x9, 0.

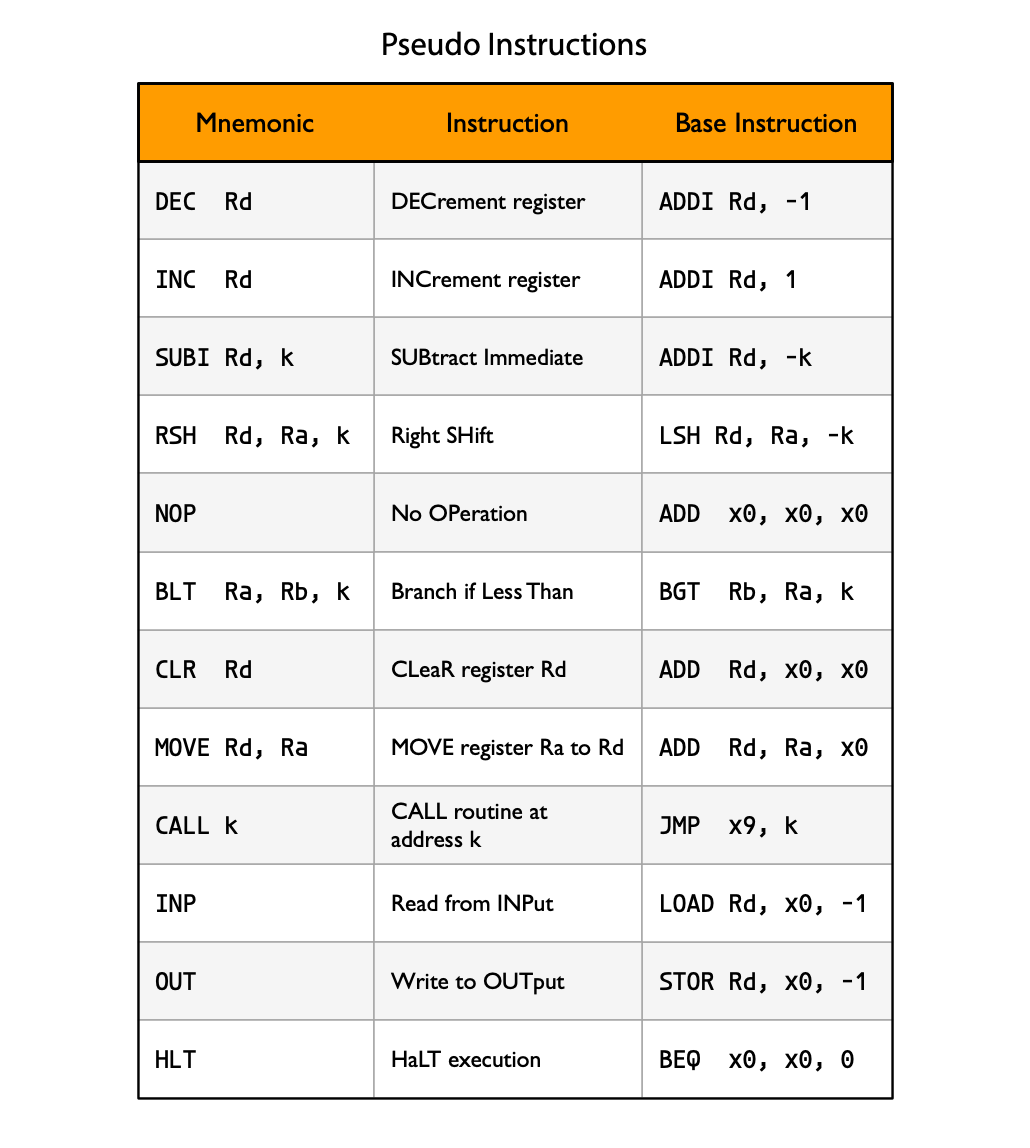
Pseudo Instructions

As I have pointed out we only have space for ten opcodes, yet if you have examined the code examples, you may conclude that there are far more than ten instructions. In fact, it looks like there are 21 instructions. What is going on? These extra elven instructions are fake, or what we call pseudo instructions. In essence, they are aliases or shorthands for one of the real instructions.

For instance, the earlier code example uses a clear instruction (CLR) several times. There is no dedicated opcode for CLR. Instead, CLR Rd is an alias for ADD Rd, x0, x0. Thus, if I write CLR x4, it translates into ADD x4, x0, x0by the assembler.

If you study the rightmost column in the pseudo instruction reference, you will see why the x0 register is so useful. Most of the pseudo instructions are made possible because x0 is always guaranteed to have the value zero.

Many architectures have an increment and decrement instruction. We don't need that either since, for instance, the INC x4 instruction can be encoded as ADDI x4, 1. Nor do we require an explicit subtract immediate, SUBI, instruction. In Calcutron-33, the pseudo instruction SUBI x4, 2 translates into ADDI x4, -2.

Shorthand versions of base instructions

The Calcutron-33 assembler does not just translate pseudo instructions to base instructions. It also lets you write shorthand versions of many instructions. For instance, if you skip a register operand when writing a load or store instruction, it will be assumed that you meant to write x0. Thus LOAD x5, 3 translates to LOAD x5, x0, 3. If instead you skip the immediate value and write LOAD x4, x2, the assembler will assume that you meant to write LOAD x4, x2, 0.

Addition and subtraction works slightly different. With only two operands, we assume that the destination register Rd is one of the source registers. Thus, instruction ADD x4, x3 translates into instruction ADD x4, x4, x3.

The JMP instruction also allows you to specify only one of the operands. If no register is specified x0 is assumed, and if no immediate value is specified we assume it is 0. In other words, JMP 42 translates into JMP x0, 42.

Input and output instructions

The INP and OUT instructions are an interesting twist. They are load and store instructions reading or writing to address -1. Of course a negative address doesn't make any sense, but if you read my treatment of negative numbers on Calcutron-33, you would know that for a 4-digit register -1 will be represented by the number 9999, since computers cannot store sign directly. We represent negative numbers by storing their complement value.

Calcutron-33 uses what is called memory-mapped I/O. That means that specific addresses are mapped to specific I/O devices. At the moment we only attach to something simulating an I/O device similar to a punched tape or network connection. However, future versions of Calcutron-33 may add other I/O devices at the high-address range.