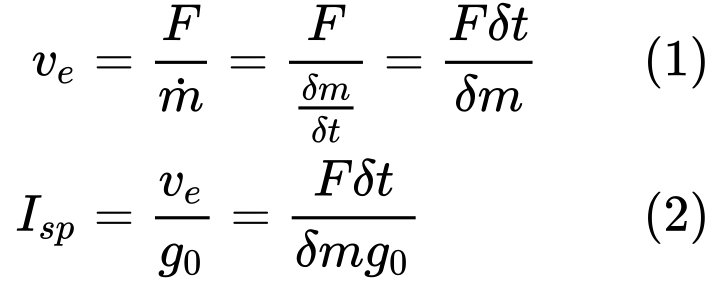The Horsepower and Gas Mileage of a Rocket Engine

Explanation of thrust, specific impulse and thrust to weight ratio (TWR) of rocket engines

We measure the efficiency of a car engine by specifying how many kilometers it will get you per liter of petroleum. Or alternatively, if you are American, how many miles you get per gallon of gasoline.

Another metric of interest is the amount of horsepower provided by the engine. It does not matter how good mileage it has if it takes forever to get anywhere.

Now imagine you go into the used rocket dealership and ask for a great rocket to fly to Mars with. You want to figure out how good the rocket is, but you cannot ask about gas mileage because that concept makes absolutely no sense when discussing the fuel efficiency of a rocket engine.

Allow me to clarify why: When you are in an orbit around a planet or moon, you keep moving in orbit, even when the engines are shut off. There is no friction in outer space. Thus, you can move as many kilometers as you like without spending any fuel! Thus, asking how many kilometers the rocket can travel on one liter of fuel cease to have meaning.

Measuring Fuel Efficiency with Specific Impulse

Instead, we specify efficiency of a rocket engine using what is called specific impulse or Isp for short. Specific impulse tells us how much one unit of propellant or fuel will change the momentum of the rocket. Momentum, p is defined as mass m multiplied by velocity v:

p = mv

The concept of momentum is important in physics because it captures the fact that the mass of a moving object matters, not merely its velocity. A small fast object will hardly move a big object, but a very heavy slow-moving object will have enough momentum to push a heavy object.

A high specific impulse means the rocket engine requires less fuel to increase the velocity of the rocket. The reason we talk about change in momentum, rather than velocity, is because the mass of the rocket matters. The same rocket engine, cannot increase the velocity of a gigantic rocket as much as it can increase the velocity of a tiny one.

Specific impulse can be defined in several ways:

In equation (1), we define the specific impulse, vₑ as a thrust relative to mass flow of propellant; Meaning how much does the rocket move for each unit of propellant? vₑ is also referred to as "effective exhaust velocity."

A popular alternative is to measure specific impulse as thrust relative to weight flow, as in equation (2). Weight is not the same as mass, rather it is the attractive force between objects with mass. We tend to abuse this terminology in daily speech. Saying: "I weigh 100 kg," is actually wrong. The correct claim is that your mass is 100 kg. Your weight would be 100 kg ⋅ 9.8 m/s² = 980 Newton.

Difference between fuel and propellant: Rockets, unlike cars, have to carry both fuel and oxygen in their tanks as there is no oxygen floating around readily available in space. The oxygen is referred to as an oxidizer.

Strictly speaking, an oxidizer doesn't need to be oxygen. For instance, Silane fuel can react with carbon-dioxide and has thus been considered as fuel for vehicles on Mars, which has a CO2 atmosphere rather than an oxygen rich atmosphere like Earth.

Thus, a more practical term for rockets is propellant. Propellant means whatever substance you use to drive the rocket engine forward.

Using Specific Impulse To Do Rocket Travel Planning

To determine where a rocket can travel in the solar system, we need to know the following:

• How much propellant is in the rocket tanks

• What is the dry mass of the rocket (mass without propellant)

• Specific impulse of the rocket engines

With this info, we can use the Tsiolkovsky rocket equation to calculate a quantity called delta-v. This is nothing more than a change in velocity. We say delta-v because it can mean a combination of increases and reductions of velocity. However, all these velocity changes have to be added up. The rocket equation can be written in two different ways:

In these two equations, the variables are defined as follows:

• Δv – Max change in velocity.

• m₀ — Initial mass of rocket, including propellant.

• mf — Final total mass, also known as dry mass. Mass of rocket without propellant.

• vₑ — Effective exhaust velocity, which is one way of measuring specific impulse.

• Isp — Specific impulse measured as force relative to weight flow.

You can think of Δv as a budget available to your rocket, which you can spend parts of to get to different parts of the solar system. Rocket travel to different parts of the solar system is composed of so-called orbital maneuvers. Every orbital-maneuver requires spending some of the Δv budget available to the rocket.

Example of a Hohmann transfer orbit from Earth orbit to Mars orbit.

Above is an example of an orbital maneuver called a Hohmann transfer. A spacecraft starts in the blue orbit and wants to reach the red orbit representing the Martian orbit around the sun. The spacecraft fires its engines to create the black elliptical orbit that intersects with Mars. At Mars, the rocket engines are fired a second time to turn the elliptical orbit into a circular orbit. Each time the engines are fired some portion of the Δv is spent.

Specific impulse of the rocket engine is one of the most important factors when determining orbital maneuvers. However, when it comes to getting into orbit from a planetary surface or de-orbiting, another rocket engine metric is more significant.

Thrust to Weight Ratio (TWR)

While specific impulse is essential to rocket engines, it is not the only thing that matters, how powerful the engine is, is also crucial. Imagine driving a really fuel-efficient car, but it has only half a horsepower. Sure, you may spend tiny amounts of fuel to go anywhere, but it will take an eternity to get anywhere.

The same goes for rocket engines. If the thrust to weight ration, TWRof the rocket is very low, then it will spend a lot of time to change its Δv. That may not matter that much to a robotic spacecraft exploring the solar system, but it matters to humans.

TWR is the force of the thrust F divided by the weight of the rocket, which is its mass m times the acceleration of gravity g on the planet you are trying to launch from.

So, one way of looking at TWR, is to think about it as acceleration measured in Gs. If TWR < 1 then your rocket cannot get off the ground because the thrust is not powerful enough to counter gravity. At TWR > 1, your rocket will ascend.

On earth when they are launching rockets they aim for a TWR of 1.25 to 1.3. In the Kerbal Space Program game, one aims for 1.5 to 3. It is an ideal game to learn about these concepts.

Ideally, the TWR should be as high as possible because then you avoid wasting lots of Δv fighting gravity (gravitational drag). If the rocket goes vertical for a time t, then your actual Δv ends up being:

But this is a gross simplification, as real rockets spend very little time going completely vertical. Instead, they perform a gravity turn, slowly tilting over until they are perpendicular to the earth. You cannot calculate total loss of Δv without taking the whole launch trajectory into account.

What prevents us from using as high TWR as possible is that air resistance (air drag) increased rapidly when you increase velocity. Thus, if you go too fast, you start wasting more energy fighting air resistance. Hence, one tries to keep thrust at 1.3 times the weight of the rocket. As propellant is spent, the weight of the rocket drops, which means you got to gradually throttle down as you ascent to orbit. Once in orbit, TWR matters much less. On planets or moons without atmosphere, you can launch with much higher TWR.

TWR and Isp Relationship

An interesting thing, you'll notice with the rocket equation, is that only the specific impulse and mass fraction matters; Meaning thrust per weight (TWR) is irrelevant with respect to how much Δv a rocket can produce. The exception is when a rocket is launched. In that case, TWR is essential.

Consequently, one can keep adding rocket engines to a rocket to increase thrust, but that will not cause the Δv to change. So more engines neither propels a rocket further nor shorter in principle.

However, engines add mass to the rocket, which screws up the mass fraction m₀/mf. Just to illustrate the problem, assume mₑ is the weight of all added engines. Assume we keep adding engines, what would happen with Δv?

From the equation, you can see that it would start approaching zero. Hence, adding more engines will reduce Δv. That is why spaceships in orbit will attempt to have as small engines as possible to improve Δvbudget. However, if too small engines are used, the orbital maneuvers will take so long time to perform that navigating the rocket becomes impractical.

On the other hand, when you launch a rocket, you want massive engines to get out of the Earth's gravity well as quickly as possible, before the gravity eats up too much of the Δv.

Summary

You need high thrust to gain a favorable TWR for launching rockets from a planetary surface. However, once in orbit propellant efficiency matters more. Thus the first stage of a multi-staged rocket tends to be optimized for high thrust, while the later stages are optimized for propellant efficiency (Isp).